Screenshot Gallery

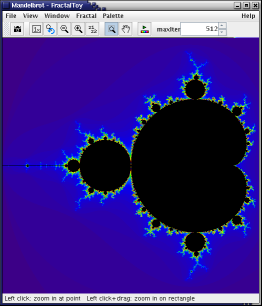
First screen: you'll see the Mandelbrot set, one of the most well known fractal shapes.

We can explore the fractal by left-clicking and dragging the mouse pointer over a "chaotic" part of the image - one that shows a lot of noise and rapid transitions in colour over a short distance. Let's choose the small, black "burr" at the left side of the image…

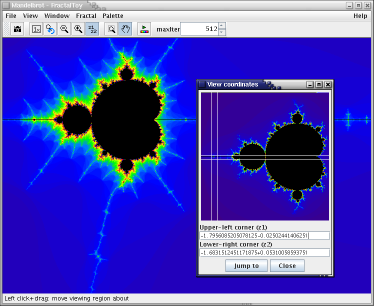
…and you'll find a shining example of the fractal's self-similarity. This pattern will keep on going ad infinitum by the way, however each incarnation differs slightly in a unique way.

Click on the z1 z2 toolbar icon to bring up the coordinates window; this will not only just show the view coordinates you're currently looking at, but also a "where am I?" reference picture that reveals your location within the entire shape.

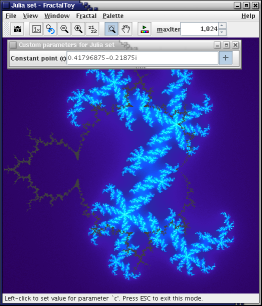
Next, let's check out the Julia set (this version uses a quadratic function). The Julia set needs a special parameter (a constant point) as part of its equation. You'll see a new toolbar pop up that lets you pick this point from the image. Click on the crosshairs toolbar icon. You'll see an outline of the Mandelbrot set superimposed. Click anywhere on the image to set a new value for this parameter.

You'll get differing results based on where you click. As the Julia set fractal is closely related to the Mandelbrot set, points that are close to (but not within) the outline will produce very interesting results, such as intricate flower, snowflake or seahorse-like shapes.

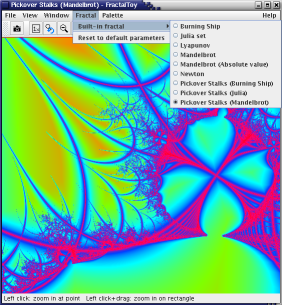
Pickover Stalks are the organic tendril-like formations created when the same fractal systems we saw before are colour-graded using a distance-from-axes function (as opposed to the previous escape-time method). Here we're looking at such a rendition of the Mandelbrot Set.

This screenshot also demonstrates the pulldown menu of fractal shapes available; just pick a new fractal and you're away; no need to play with puzzling parameters to try and get something interesting showing.

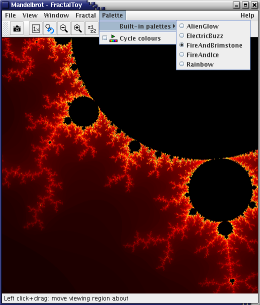
Each fractal has a number of palettes configured to bring out all the fine details. There's also a cycle colours animation gimmick that lets you watch the bands of colours pulsate throughout the depths of the fractal shape.

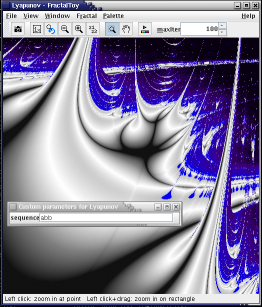
Markus-Lyapunov fractals are generated from a 2D logistic map that simulates a population where individual points rapidly alternate between two values A & B according to a given periodic sequence. A special measure known as the Lyapunov exponent is used to classify how quickly the trajectories of each point diverge; this grades the image into portions of order (silver) and chaos (blue).

It is known for generating remarkably sophisticated shapes from a very simple formula, such as metallic bars folding over each other, fleets of alienesque spaceships, and the famous Zircon Zity (try the sequence "bbbbbbaaaaaa").